توابع وام در اکسل — راهنمای کاربردی

توابع وام در اکسل — راهنمای کاربردی

نرم‌افزارهای صفحه گسترده (Spread Sheet) برای کاربران حوزه حسابداری و امور مالی توسعه یافتند. به همین علت، انجام محاسباتی مانند دفاتر حسابداری و جداول و گزارشات مالی در آن‌ها به سهولت صورت می‌گیرد. از طرف دیگر وجود توابع محاسباتی که وابسته به شاخص‌های مالی هستند به محبوبیت نرم‌افزارهای صفحه گسترده‌ها اضافه می‌کند. امروزه یکی از پرطرفدارترین نرم‌افزارهای صفحه گسترده، اکسل مایکروسافت(Microsoft Excel) است که کاربران زیادی در سراسر جهان دارد. در این نوشتار به بررسی توابع وام در اکسل خواهیم پرداخت و با ذکر مثال‌هایی، نحوه انجام محاسبات با این گونه توابع را معرفی خواهیم کرد. البته نرم‌افزارهای صفحه گسترده دیگر مانندکاربرگ گوگل (Google Sheet) و اوپن آفیس (Open Office) مربوط به شرکت آپاچی (Apache) نیز در این بین، طرفداران خود را دارند.

 

 

توابع وام در اکسل

قدرت و کارایی اکسل، در انجام محاسبات نهفته است. فرمول نویسی و استفاده از توابع درونی اکسل، انجام بسیاری از کارها را ساده‌تر و البته سریع‌تر می‌کند. برای دسترسی به توابع مالی در اکسل، کافی است از برگه Formula گزینه Financial را انتخاب کنید. لیست طولانی از توابع مالی در اکسل ظاهر خواهد شد که شامل ۵۵ تابع مختلف است. در این قسمت به بعضی از توابع مربوط با وام خواهیم پرداخت که شامل IPMT ،PMT و PPMT است و خصوصیات محاسباتی هر یک را مورد مطالعه قرار می‌دهیم. البته در این بین به توابعی دیگری که با این موضوع مرتبط هستند نیز آشنا خواهیم شد. مثلا توابع PV و RATE همچنین NPER که به عنوان پارامتر در تابع PMT‌ به کار می‌روند، نیز مورد بحث قرار خواهند گرفت، زیرا این توابع با یکدیگر در یک رابطه ریاضی قرار دارند. این رابطه که به شکل یک معادله است، در زیر دیده می‌شود.

$$large begin{cases}pv times (1+rate)^{nper}+pmt(1+ratetimes type)times dfrac{(1+rate)^{nper}-1}{rate}+fv=0 & rate neq 0\(pmttimes nper)+pv+fv=0 & rate =0end{cases}$$

رابطه ۱

محاسبه اقساط یک وام با تابع PMT

فرض کنید به شما، صندوقی معرفی شده که یک وام با مبلغ و بهره مشخص می‌دهد. مبلغ هر قسط وابسته به تعداد اقساط یا دوره‌ای است که قسط‌ها را پرداخت می‌کنید. با توجه به درآمد ماهانه‌ای که دارید می‌خواهید تصمیم بگیرید که کدام مبلغ قسط (و البته تعداد ماه‌های بازپرداخت) برایتان مناسب‌تر است. در این بین تابع PMT‌ به کمک شما می‌آید و می‌تواند سناریو‌های مختلفی برحسب تعداد اقساط و مبلغ قسط ماهانه به شما ارائه دهد.

 

به طور دقیق‌تر می‌توان گفت که این تابع قابلیت محاسبه میزان یا مقدار قسط (Payment) یک وام با بهره یا سود ثابت و البته مبلغ بازپرداخت ثابت را دارد. شکل و پارامترهای این تابع به صورت زیر است.

$$large PMT;(rate; ,nper; ,pv; ,[fv]; ,[type];)$$

استفاده از پارامترهای fv و type برای محاسبه این تابع اختیاری است و اکسل مقدارهای پیش‌فرض برای آن‌ها در نظر گرفته است ولی اگر مقدار آن‌ها را تعیین کنید، ممکن است نحوه محاسبات تغییر کند.

توجه داشته باشید واحد زمانی برای پارامترهای این تابع باید یکسان باشد، به این معنی که نرخ بهره و تعداد اقساط باید با یک واحد زمانی سنجیده شوند. برای مثال اگر می‌خواهید مقدار قسط ماهانه وامی را محاسبه کنید، پارامترهای دوره بازپرداخت و نرخ بهره وام باید ماهانه باشند. از طرفی در محاسبات مربوط به این تابع، مقدار اقساط در طول دوره بازپرداخت یکسان در نظر گرفته می‌شود.

در ادامه پارامترهای این تابع را معرفی و در مورد خصوصیات هر یک توضیحاتی ارائه خواهیم کرد.

پارامتر	مشخصات	توضیحات
rate	نرخ بهره وام یا نرخ سود در سرمایه‌گذاری	از لحاظ زمانی، هم واحد با زمان باز پرداخت اقساط
nper	دوره بازپرداخت	از لحاظ زمانی، هم واحد با زمان باز پرداخت اقساط
pv	مبلغ وام یا میزان سرمایه گذاری جاری	با توجه به ماهیت بدهکار و بستانکاری، مقداری مثبت یا منفی است.
fv	ارزش آتی سرمایه	ارزش وام (یا سرمایه‌گذاری) در پایان دوره باز پرداخت
type	نوع پرداخت	دو مقداری (۰=بازپرداخت در پایان هر دوره و ۱= بازپرداخت در ابتدای هر دوره باز پرداخت)

به منظور واضح‌تر شدن خصوصیات و ویژگی‌های هر یک از این پارامترها، توضیحاتی نیز در ادامه آمده است.

• نرخ بهره وام-سرمایه‌گذاری (rate): در این قسمت باید نرخ بهره وام دریافتی یا مبلغ سرمایه‌گذاری را مشخص کنید. البته توجه داشته باشید که اگر می‌خواهید اقساط ماهانه وام را به وسیله این تابع محاسبه کنید، باید این نرخ را هم به صورت ماهانه وارد کنید. برای مثال اگر نرخ بهره یک وام ۱۸٪ در سال است، برای محاسبه اقساط وام ماهانه باید نرخ بهره سالانه را بر ۱۲ تقسیم کنید تا نرخ بهره ماهانه بدست آید. واضح است که این عدد باید به صورت درصدی یا اعشاری وارد شود. در صورتی که از این تابع به منظور تعیین درآمدهای در یک طرح سرمایه‌گذاری استفاده می‌کنید، این مقدار می‌تواند نرخ سود یک سرمایه‌گذاری نیز باشد که قرار است سود آن به صورت ماهانه پرداخت شود.
• دوره بازپرداخت (nper): این پارامتر بیانگر طول دوره بازپرداخت وام است. به این معنی که باید تعداد سال یا ماه‌هایی که وام مستهلاک می‌شود را در این پارامتر وارد کنید. باز هم توجه داشته باشید که اگر می‌خواهید اقساط را برحسب ماه محاسبه کنید باید دوره بازپرداخت را هم ماهانه وارد کنید تا اکسل در انجام محاسبات دچار مشکل نشود. واضح است که این مقدار نیز عددی نامنفی است. باز هم اگر از این تابع برای سرمایه‌گذاری استفاده کرده‌اید، این پارامتر، دوره سرمایه‌گذاری را مشخص می‌کند.
• مبلغ وام یا میزان سرمایه‌گذاری جاری (pv): در این پارامتر مبلغ وام را وارد می‌کنیم. توجه داشته باشید که اگر می‌خواهید قسط وام را برحسب ریال دریافت کنید، باید این مقدار را نیز برحسب ریال ثبت کنید. البته از یاد نبرید که مقدار مثبت برای این پارامتر باعث ایجاد مقدار منفی برای مبلغ قسط یا سود ماهانه وام خواهد شد. زیرا وام را دریافت ولی قسط را پرداخت می‌کنید. از طرفی اگر هدف سرمایه‌گذاری است باید مقدار این پارامتر را در تابع منفی وارد کنید، زیرا مبلغی است که از دارایی شما کسر می‌شود. به این ترتیب نتیجه محاسبه تابع pmt‌ مثبت شده و به معنی دریافت مبلغ حاصل از سرمایه‌گذاری است.
• ارزش آتی سرمایه (fv): اگر لازم باشد می‌توانید ارزش این سرمایه‌گذاری (مبلغ وام که در pv ثبت شده) را در پایان دوره بازپرداخت مشخص کنید. پارامتر fv ارزش آتی سرمایه دریافتی را پس از گذشت nper واحد زمانی مشخص می‌کند. اگر می‌خواهید بالانس مثبت داشته باشید ملبغ مورد نظر را در fv وارد کنید. در صورتی که این مقدار وارد نشود، اکسل به طور پیش‌فرض مقدار صفر را در نظر گرفته و حساب را تسویه می‌کند. برای مثال فرض کنید صندوقی از شما می‌خواهد که در آن سرمایه‌گذاری کنید. این صندوق تضمین می‌کند با سود مشخص در پایان دوره سرمایه‌گذاری، ۱۰ میلیون تومان به شما پرداخت خواهد کرد. به این ترتیب برای پیدا کردن مبلغ پرداختی ماهانه در این صندوق از تابع PMT استفاده کرده و مقدار pv را صفر و fv را همان ۱۰ میلیون تومان در نظر می‌گیریم. همچنین اگر می‌خواهید با دریافت وامی که در pv مشخص شده در پایان دوره بازپرداخت وام، ذخیره‌ای هم در بانک وام دهنده داشته باشید، آن مبلغ را به عنوان پارامتر fv وارد می‌کنید.
• نوع بازپرداخت (type): اگر مبلغ اقساط را در پایان هر دوره (مثلا در پایان هر ماه) پرداخت می‌کنید می‌توانید این پارامتر را صفر در نظر بگیرید. البته اگر مقداری برای type وارد نکنید به طور خودکار صفر در نظر گفته شده و مشخص می‌شود که اقساط در پایان هر دوره پرداخت می‌شوند. اگر می‌خواهید شیوه محاسبه بازپرداخت براساس آغاز دوره انجام شود، مقدار این پارامتر را برابر با ۱ در نظر بگیرید. به این ترتیب مشخص می‌کنید که هر قسط در ابتدای ماه پرداخت می‌شود. واضح است که با این کار به محض دریافت وام، قسط اول از آن کسر خواهد شد.

 

مثال 1: فرض کنید یک وام پنج میلیون تومانی قرار است از یک بانک با بهره ۱۰٪ سالانه دریافت کنید. تعداد اقساط و مبلغ قسط در اختیار شما است. به کمک چند سناریو می‌خواهیم بهترین وضعیت را با توجه به درآمد ماهانه و البته مبلغ بازگشتی وام، بدست آوریم. برای این محاسبات، کاربرگی به صورت زیر تشکیل داده‌ایم.

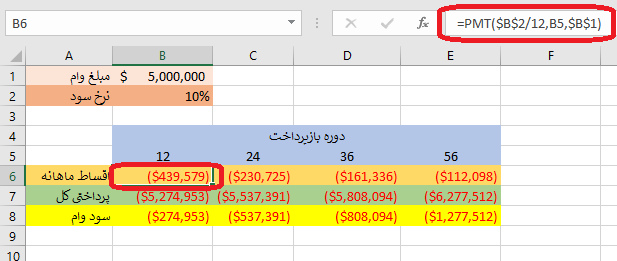
مبلغ قسط ماهانه در سطر ششم و با رنگ نارنجی مشخص شده است. فرمول مربوط به این بخش به صورت زیر است.

$$large PMT($B$2/12,B5,$B$1)$$

همانطور که دیده می‌شود، نرخ سود وام را بر ۱۲ تقسیم کرده‌ایم زیرا قرار است تابع PMT، اقساط ماهانه را مشخص کند. از طرفی از آنجایی که مبلغ وام را مثبت وارد کرده‌ایم، مقدار قسط، منفی محاسبه شده است زیرا وام را دریافت و اقساط را پرداخت می‌کنیم.

نکته: توجه داشته باشید که علامت‌های $ در آدرس هر یک از سلول‌ها در فرمول به منظور مطلق کردن آن به کار رفته تا هنگام کپی کردن در سلول‌های مجاور، آدرس تغییر نکند.

در پایین دوره بازپرداخت که به صورت ماهانه مشخص شده،‌ اقساط ماهانه محاسبه شده است. برای محاسبه پرداختی کل نیز تعداد اقساط را در مبلغ هر قسط ضرب کرده‌ایم زیرا می‌دانیم که در هر دوره بازپرداخت، قسط ثابت است. در ادامه فرمول‌های محاسباتی آورده شده است. در سطر اول فرمول برای پرداخت کل و در سطر دوم نیز سود وام برای اقساط ۱۲ ماهه مورد محاسبه قرار گرفته است.

$$large =B6times B5\ large=B7+$B$1$$

محاسبه نرخ سود وام با تابع RATE

همانطور که در قسمت قبل دیدید، در تابع PMT، پارامتری به عنوان نرخ سود وام (سرمایه‌گذاری) وجود دارد که با RATE نشان داده می‌شود. این بار می‌خواهیم مسئله وام را براساس نرخ سود حل کنیم. فرض کنید یک وام به شما معرفی شده است که تعداد دوره بازپرداخت و اقساط آن مشخص است. می‌خواهید نرخ سود وام را محاسبه کنید. یا اگر با سرمایه‌گذاری مواجه هستیم، می‌خواهیم بدانیم اگر مبلغ PV را در یک طرح، سرمایه‌گذاری کنیم و از این بابت دریافتی‌هایی ثابت و برابر با PMT داشته باشیم نرخ سود چقدر خواهد بود؟ البته توجه داشته باشید که پرداخت‌ها در دوره‌هایی با فاصله‌های زمانی یکسان صورت می‌گیرد.

در این حالت تابع RATE می‌تواند راهگشا باشد. پارامترهای این تابع به صورت زیر است.

$$large RATE(nper; ,pmt; ,pv; ,[fv]; ,[type];)$$

نکته: نحوه ارتباط بین پارامترهای این تابع، مطابق با رابطه ۱ است. البته باید توجه داشته باشید که در اینجا علامت پارامتر pmt و pv باید عکس یکدیگر باشند. یعنی اگر pv‌ مثبت باشد، حتما باید pmt را منفی وارد کنید.

مثال ۲: با توجه به داده‌های مثال ۱، اگر طول دوره بازپرداخت ۵۶ ماه باشد، با مبلغ بازپرداخت ماهانه $$112098$$، نرخ سود وام به طور سالانه طبق فرمول زیر محاسبه خواهد شد.

$$large =RATE(56,-112098,B1)times 12=0.09999approx 0.10$$

همانطور که می‌بینید، نتیجه تابع RATE در ۱۲ ضرب شده است. زیرا می‌خواهیم سود سالانه را محاسبه کنیم. با توجه به اینکه همه ارقام در اینجا برحسب ماه نوشته شده‌اند، نرخ سود وام ماهانه خواهد بود و برای بدست آوردن نرخ سود سالانه، حاصل را در ۱۲ ضرب کرده‌ایم. نتیجه این محاسبات برابر با ۱۰٪ است. پس سود این وام ۱۰٪ سالانه خواهد بود.

محاسبه تعداد اقساط یک وام با NPER

این بار در نظر بگیرید که مبلغ وام و اقساط آن به همراه سود مشخص است و می‌خواهیم تعداد دوره بازپرداخت را محاسبه کنیم. به این ترتیب PV ،PMT ،RATE مشخص بوده و می‌خواهیم NPER را بدست آوریم. پارامترهای این تابع به صورت زیر است.

$$large NPER(rate; ,pmt; ,pv; ,[fv]; ,[type];)$$

مثال ۳: داده‌های مربوط به مثال ۱ را در نظر بگیرید. می‌دانیم که مبلغ وام ۵ میلیون تومان و سود آن ۱۰٪ سالانه است. می‌خواهیم بدانیم که اگر مبلغ پرداخت ماهانه برابر با 450 هزار تومان باشد، تعداد اقساط وام چند ماه خواهد بود؟

در تصویر زیر پنجره پارامترهای تابع NPER برای پاسخ به این سوال،‌ دیده می‌شود.

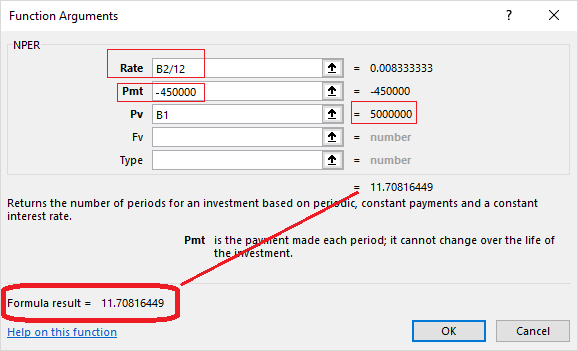
همانطور که در قسمت نتیجه فرمول (Formula Result) مشاهده می‌کنید، تعداد ماه‌ها برابر با $$11.708$$ است. البته همین مقدار را در قسمت انتهایی پارامترها نیز می‌بینید. مشخص است که نرخ بهره را بر ۱۲ تقسیم کرده‌ایم تا نرخ ماهانه بدست آید. همچنین مبلغ پرداخت ماهانه را نیز منفی وارده کرده‌ایم و از طرفی نیز ارزش وام مثبت در نظر گرفته شده است. از آنجایی که تعداد ماه‌ها، عدد صحیح بدست نیامده، معلوم می‌شود که اگر تعداد اقساط را ۱۲ ماهه در نظر بگیریم، مبلغ قسط آخر از بقیه‌ ماه‌ها کمتر خواهد بود.

محاسبه ارزش فعلی سرمایه‌گذاری با تابع PV

فرض کنید، قرار است در یک صندوق با سود ثابت، سرمایه‌گذاری کنید. البته پرداخت‌ شما برای سرمایه‌گذاری به صورت دوره‌ای یا قسطی صورت می‌گیرد؛ در هر دوره نیز مبلغ پرداختی شما ثابت است. می‌خواهیم بدانیم مقدار نهایی این سرمایه‌گذاری در زمان جاری چیست؟! در اینجا باید از تابع PV استفاده کنیم. پارامترهای این تابع شبیه پارامترهای تابع PMT هستند.

$$large PV;(rate; ,nper; ,pmt; ,[fv]; ,[type];)$$

تابع PV ارزش یک سرمایه‌گذاری با پرداخت‌های ثابت در هر دوره را محاسبه می‌کند. توجه داشته باشید که اگر pmt‌ مقداری مثبت باشد، مقدار PV منفی خواهد بود و برعکس اگر pmt را منفی وارد کنید (از آنجایی که مبلغ را پرداخت می‌کنید) دریافتی شما پس از رسیدن به آخرین دوره پرداخت با توجه به نرخ سودآوری، مقداری مثبت است.

مثال 4: فرض کنید قرار است در یک صندوق سرمایه‌گذاری، سالانه ۱ میلیون تومان به مدت ۱۰ سال سرمایه‌گذاری کنید. صندوق به شما تضمین داده است که نرخ سود این سرمایه‌گذاری ۲۰٪ در سال است. دوره سررسید این سرمایه‌گذاری ۵ سال در نظر گرفته شده است. در این صورت میزان دریافتی مورد انتظار، در پایان دوره از این صندوق مطابق با رابطه زیر خواهد بود.

$$large PV(20%,10,-1000000,0,0)= 4192472.085$$

مشخص است از آنجایی که مقدار پرداخت‌ها را منفی وارد کرده‌ایم، درآمد حاصل از سرمایه‌گذاری مثبت بدست آمده است. پس با توجه به نتیجه، مشخص است پولی که در آینده خواهید داشت به ارزش قیمت امروز، حدود ۴ میلیون تومان می‌ارزد. شاید بتوان در این مثال ۲۰ درصد را همان نرخ تورم سالانه در نظر گرفت.

محاسبه اصل و سود از هر پرداخت با توابع PPMT و IPMT

دو تابع دیگر نیز با تابع PMT‌ همراه و همگام هستند. هر قسط وام از دو بخش تشکیل شده است. قسمتی از این پرداخت، اصل مبلغ وام را تشکیل می‌دهد و قسمت دیگر متعلق به سود وام است. تابع PPMT بخش اصل و تابع IPMT بخش سود از هر پرداخت را مشخص می‌کنند. هر دو این توابع دارای پارامترهای یکسانی هستند و تفاوت آن‌ها فقط در نحوه محاسبه است. بنابراین در اینجا فقط پارامترهای IPMT را معرفی می‌کنیم.

$$large IPMT;(rate; ,per; ,nper; ,pv; ,[fv]; ,[type];)$$

همانطور که مشخص است، تنها پارامتر per در تابع IPMT نسبت به PMT‌ اضافه شده است که نشان دهنده دوره‌ای است که می‌خواهید سود وام را در آن محاسبه کنید. شرط هم واحد بودن زمان برای پارامترهای این تابع نیز به قوت خود باقی است.

مثال 5: براساس داده‌های مربوط به مثال ۱، جدول زیر را تشکیل داده‌ایم تا بخش‌های سود و اصل از پرداخت هر قسط در ۱۲ ماه سال مشخص شود. همانطور که در تصویر زیر دیده می‌شود، مجموع اصل و سود پرداختی از وام با کل مبلغ قسط در هر ماه برابر است. به این معنی که مجموع دو مقدار حاصل از IPMT و PPMT‌، همیشه با مقدار کل قسط که با PMT محاسبه شده، یکسان است.

همانطور که در این جدول دیده می‌شود، در دوره‌های ابتدایی پرداخت وام، سهم بیشتری از پرداخت کل، مربوط به سود بوده و مبلغ اصل وام کمتر از سود است. ولی هر چه به پایان دوره نزدیک‌تر می‌شویم، سهم سود کاسته شده زیرا بیشتر مبلغ مربوط به سود را پرداخت کرده‌ایم و بیشتر مبلغ قسط، مربوط به بخش اصل وام است.

نکته: PMT مخفف کلمه Payment‌ به معنی پرداخت است. همچنین IPMT‌ نیز مخفف Interest Payment به معنی «سود پرداخت» و PPMT نیز مخفف Principle Payment یا «اصل پرداخت» است. گاهی به سود پرداخت، فرع نیز می‌گویند. بنابراین هر پرداخت از یک بخش اصل و یک بخش فرع تشکیل می‌شود.

خلاصه و جمع‌بندی

توابع مالی زیادی در اکسل وجود دارند که البته شاید همه آن‌ها به کار یک موسسه مالی نیایند. در اینجا با توابع مربوط به وام و اقساط و همچنین سود وام در اکسل آشنا شدیم. به کمک مثال‌هایی نیز نحوه به کارگیری اکسل در انجام این گونه محاسبات را فرا گرفتیم. هماهنگی زمانی بین پارامترهای توابع مالی از اهمیت زیادی برخوردار است و عدم رعایت آن، منجر به دریافت پاسخ‌های اشتباه خواهد شد. همچنین توجه به علامت مقادیر در این گونه توابع نیز مهم بوده و ممکن است با عدم توجه به این موضوع، نتایج نادرستی بدست آید.منبع:فرادرس